Logistic Regression using the Pyro

Here we implement Logistic Regression using the Pyro library.

import numpy as np
import matplotlib.pyplot as plt
import torch
import seaborn as sns
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split

sns.set_context("notebook")
try:
    import pyro
except ImportError:
    %pip install pyro-ppl
    import pyro
import pyro.distributions as dist
from pyro.infer import MCMC, NUTS, Predictive

X, y = make_moons(n_samples=100, noise=0.3, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.2, random_state=42)
X_train = torch.tensor(X_train).float()
y_train = torch.tensor(y_train).float()
X_test = torch.tensor(X_test).float()
y_test = torch.tensor(y_test).float()
X_train.shape, y_train.shape,X_test.shape, y_test.shape

(torch.Size([80, 2]), torch.Size([80]), torch.Size([20, 2]), torch.Size([20]))

# Separate data points by class
class_0 = X[y == 0]
class_1 = X[y == 1]

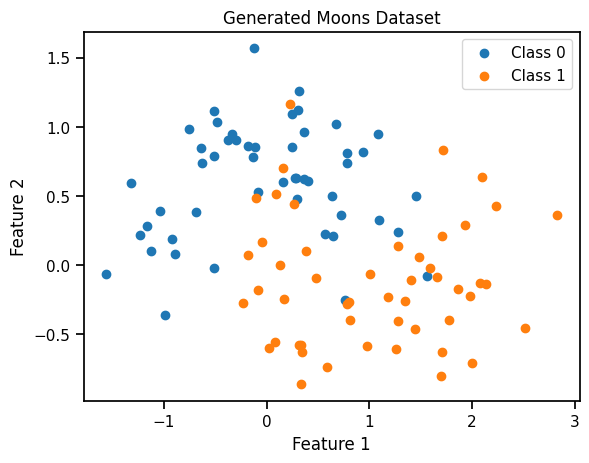
# Create a scatter plot
plt.scatter(class_0[:, 0], class_0[:, 1], label="Class 0", marker='o')
plt.scatter(class_1[:, 0], class_1[:, 1], label="Class 1", marker='o')

plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Generated Moons Dataset")
plt.legend()
plt.show()

def logistic_model(X, y):
    # sample from prior
    w = pyro.sample(
      'w', dist.Normal(torch.zeros(X.shape[1]), torch.ones(X.shape[1]))
    )
    b = pyro.sample(
      'b', dist.Normal(torch.zeros(1), torch.ones(1))
    )
    with pyro.iarange('data', X.shape[0]):
        model_logits = torch.matmul(X, w) + b
        pyro.sample('obs', dist.Bernoulli(logits=model_logits), obs=y)

We use NUTS MCMC sampling to sample the posterior and take 1000 samples for posterior distribution and use 500 samples as burn/warm up.

nuts_kernel = NUTS(logistic_model, adapt_step_size=True)
mcmc = MCMC(nuts_kernel, num_samples=1000, warmup_steps=500)
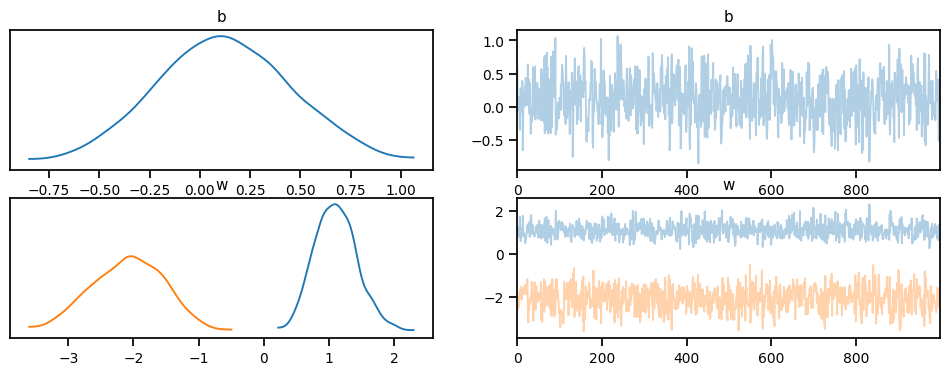
mcmc.run(X_train, y_train)

Warmup:   0%|          | 3/1500 [00:00, 25.77it/s, step size=1.20e-01, acc. prob=0.333]Sample: 100%|██████████| 1500/1500 [00:32, 46.05it/s, step size=6.50e-01, acc. prob=0.929] 

posterior_samples = mcmc.get_samples()

Following are the trace plots for the parameters of the posterior distribution.

import arviz as az

idata = az.from_pyro(mcmc)
az.plot_trace(idata, compact=True);

c:\Users\Dell\AppData\Local\Programs\Python\Python311\Lib\site-packages\arviz\data\io_pyro.py:157: UserWarning: Could not get vectorized trace, log_likelihood group will be omitted. Check your model vectorization or set log_likelihood=False
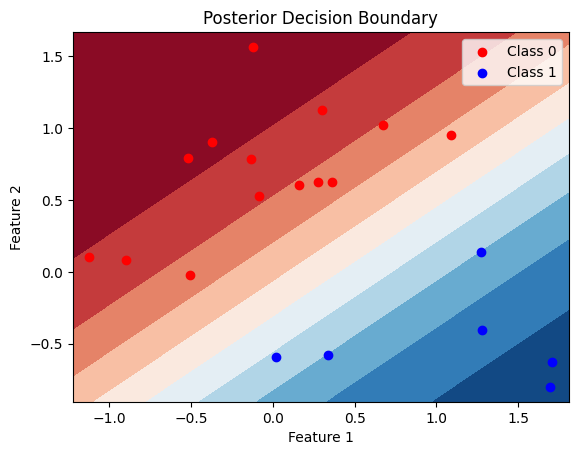
  warnings.warn(

posterior_samples['w'].mean(0), posterior_samples['b'].mean(0)

(tensor([ 1.1069, -2.0874]), tensor([0.1179]))

posterior_samples['w'].std(0), posterior_samples['b'].std(0)

(tensor([0.3259, 0.5515]), tensor([0.3369]))

Ploting the decision boundry for the test data

# Define a function to plot the decision boundary
def plot_decision_boundary(X, y, posterior_samples, title="Posterior Decision Boundary"):
    # Create a meshgrid of points for the entire feature space
    x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
    y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
    xx, yy = torch.meshgrid(torch.linspace(x_min, x_max, 100), torch.linspace(y_min, y_max, 100))

    # Flatten the meshgrid for prediction
    grid = torch.cat((xx.reshape(-1, 1), yy.reshape(-1, 1)), dim=1)

    # Get the number of posterior samples
    num_samples = len(posterior_samples['w'])

    # Plot the posterior decision boundary for each sample
    for i in range(num_samples):
        w = posterior_samples['w'][i]
        b = posterior_samples['b'][i]

        # Calculate the logits and probabilities
        logits = torch.matmul(grid, w) + b
        probs = 1 / (1 + torch.exp(-logits))
        probs = probs.detach().numpy().reshape(xx.shape)

        # Plot the decision boundary
        # plt.contourf(xx, yy, probs, levels=[0, 0.5, 1], alpha=0.2, cmap=plt.cm.RdBu)
        plt.contourf(xx, yy, probs, 10, cmap=plt.cm.RdBu)
    # Plot the data points
    plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], label="Class 0", marker='o', color = 'r')
    plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], label="Class 1", marker='o', color = 'b')

    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")
    plt.title(title)
    plt.legend()
    plt.show()

# Plot the decision boundary on the test data
plot_decision_boundary(X_test, y_test, posterior_samples)